Bạn có bao giờ cảm thấy choáng ngợp trước những bài toán hình học không gian đầy rẫy đường nét và hình khối rối rắm? Đừng lo lắng, hãy tưởng tượng việc giải toán như “vén màn sương mù”, và “cách tọa độ hóa” chính là “ánh đuốc” soi sáng con đường chinh phục hình học không gian. Giống như việc “định vị GPS” cho từng điểm, đường thẳng, mặt phẳng trong không gian, phương pháp này giúp bạn chuyển hóa những hình ảnh trừu tượng thành những con số cụ thể, từ đó giải quyết bài toán một cách logic và hiệu quả.
Ngay sau đây, “HỌC LÀM” sẽ bật mí cho bạn “bí kíp” toạ độ hóa, giúp bạn “hóa rồng” trong hình học không gian, chinh phục mọi kỳ thi một cách dễ dàng!
## Hiểu Rõ Bản Chất “Toạ Độ Hoá”
Trước khi bắt tay vào giải toán, hãy cùng “HỌC LÀM” “vén màn bí mật” về toạ độ hóa trong hình học không gian.
Toạ độ hóa, như tên gọi của nó, là việc thiết lập một hệ trục tọa độ Oxyz trong không gian và gán cho mỗi điểm một bộ ba số (x; y; z) đại diện cho vị trí của nó trong hệ trục đó.
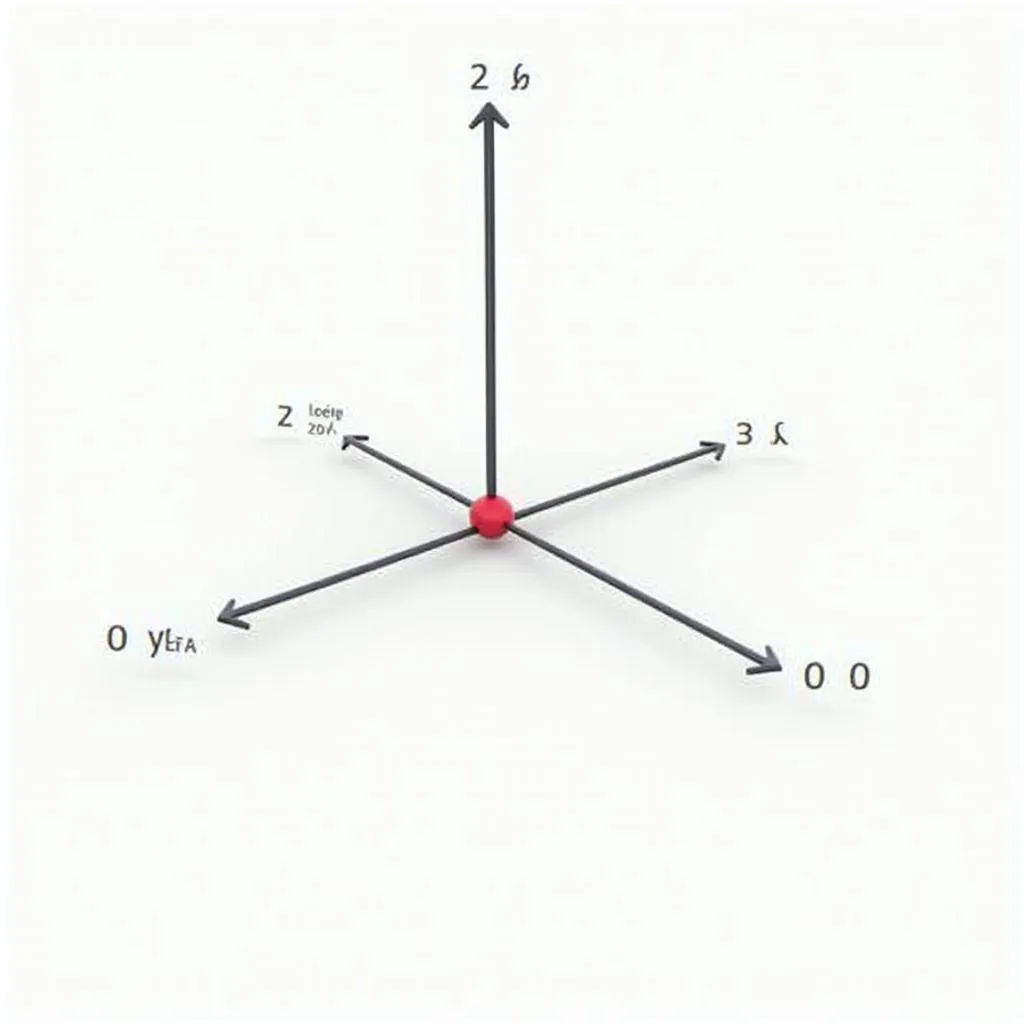 Hệ trục tọa độ trong không gian
Hệ trục tọa độ trong không gian
Tương tự, đường thẳng và mặt phẳng cũng có thể được biểu diễn bằng phương trình toán học dựa trên hệ trục tọa độ này.
## “Bí Kíp” Toạ Độ Hoá Trong Hình Học Không Gian
Để “thuần thục” phương pháp toạ độ hóa, bạn cần nắm vững một số “bí kíp” sau:
### 1. Xác Định Hệ Trục Toạ Độ Phù Hợp
Việc lựa chọn hệ trục toạ độ Oxyz sao cho phù hợp với bài toán là bước đầu tiên và vô cùng quan trọng. Một hệ trục được chọn khéo léo sẽ giúp đơn giản hóa các phép tính và rút ngắn thời gian giải toán.
### 2. “Biên Dịch” Hình Ảnh Thành Phương Trình
Sau khi đã có hệ trục tọa độ, bạn cần “dịch” các yếu tố hình học trong bài toán thành phương trình tương ứng.
Ví dụ:
- Điểm: Mỗi điểm trong không gian sẽ được xác định bởi một bộ ba số (x; y; z).
- Vectơ: Với hai điểm A(xA; yA; zA) và B(xB; yB; zB), vectơ AB sẽ có tọa độ là (xB – xA; yB – yA; zB – zA).
- Đường thẳng: Một đường thẳng có thể được xác định bởi một điểm và vectơ chỉ phương.
- Mặt phẳng: Một mặt phẳng có thể được xác định bởi một điểm và vectơ pháp tuyến.
 Phương trình đường thẳng và mặt phẳng
Phương trình đường thẳng và mặt phẳng
### 3. Ứng Dụng Công Thức Và Tính Toán
Hình học không gian cung cấp cho chúng ta một “kho tàng” các công thức tính toán liên quan đến điểm, đường thẳng, mặt phẳng.
Ví dụ:
- Khoảng cách giữa hai điểm.
- Góc giữa hai đường thẳng.
- Khoảng cách từ một điểm đến một mặt phẳng.
Bạn cần nắm vững các công thức này để giải quyết các bài toán một cách hiệu quả.
### 4. “Phản Dịch” Kết Quả Toán Học Thành Hình Ảnh
Sau khi đã tính toán và tìm ra kết quả, bạn cần “phản dịch” chúng trở lại thành hình ảnh để hình dung rõ hơn về mối quan hệ giữa các yếu tố trong không gian.
## Ứng Dụng Thực Tiễn Của Toạ Độ Hoá
Phương pháp toạ độ hóa không chỉ là “chìa khóa” giúp bạn chinh phục các bài toán hình học không gian trên lớp học mà còn có rất nhiều ứng dụng trong thực tế.
Ví dụ:
- Trong lĩnh vực xây dựng, toạ độ hóa được sử dụng để thiết kế bản vẽ, tính toán kết cấu công trình.
- Trong lĩnh vực hàng không, toạ độ hóa giúp xác định vị trí, hướng đi của máy bay.
- Trong lĩnh vực đồ họa máy tính, toạ độ hóa được sử dụng để tạo hình ảnh 3D, mô phỏng chuyển động.
## Mở Rộng Kiến Thức Với “HỌC LÀM”
Ngoài cách tính điểm tín chỉ đại học, “HỌC LÀM” còn cung cấp cho bạn nhiều kiến thức bổ ích khác như: cách tính xếp loại tốt nghiệp đại học, cách viết chuỗi phản ứng hóa học lớp 11, hay cách đánh công thức hóa học trên powerpoint.
## Kết Luận
“Cách tọa độ hóa trong hình học không gian” là một phương pháp hữu ích giúp bạn giải quyết các bài toán một cách logic, khoa học và hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích và “bí kíp” để tự tin chinh phục hình học không gian.
Hãy liên hệ với chúng tôi qua số điện thoại 0372888889 hoặc đến địa chỉ 335 Nguyễn Trãi, Thanh Xuân, Hà Nội để được tư vấn chi tiết hơn. Đội ngũ “HỌC LÀM” luôn sẵn sàng hỗ trợ bạn 24/7.

