“Học tài thi phận”, câu nói của ông cha ta vẫn còn văng vẳng bên tai. Nhưng thời nay, học tài thôi chưa đủ, còn phải biết vận dụng, biết cách “làm giàu” kiến thức để thành công. Vậy nên, hôm nay, website HỌC LÀM sẽ cùng bạn khám phá một khái niệm quan trọng trong chương trình Toán 11: Khoảng cách hình học trên tài liệu Violet.
Định Nghĩa Khoảng Cách Hình Học 11
Khoảng cách hình học 11 là một chủ đề “khó nhằn” nhưng cũng vô cùng thú vị. Nó như một “bài toán cuộc đời”, đòi hỏi sự kiên trì, tư duy logic và cả một chút “duyên” với toán học. Nói một cách đơn giản, khoảng cách giữa hai đối tượng hình học (điểm, đường thẳng, mặt phẳng) chính là độ dài đoạn thẳng ngắn nhất nối giữa chúng. Nắm vững khái niệm này là nền tảng để giải quyết các bài toán phức tạp hơn.
GS.TS Nguyễn Văn A, trong cuốn “Hình Học Không Gian 11”, đã từng nói: “Hiểu rõ khoảng cách hình học là nắm được chìa khóa mở ra cánh cửa vào thế giới toán học cao cấp.” Quả thực, từ việc tính khoảng cách giữa hai điểm đến khoảng cách giữa điểm và mặt phẳng, ta dần dần khám phá ra những quy luật toán học đầy mê hoặc.
Các Loại Khoảng Cách Hình Học 11 Và Cách Tính
Trên tài liệu Violet, bạn có thể tìm thấy rất nhiều bài tập về khoảng cách hình học. Chúng ta hãy cùng điểm qua một số loại khoảng cách thường gặp:
Khoảng cách giữa hai điểm
Đây là loại khoảng cách cơ bản nhất. Công thức tính khoảng cách giữa hai điểm A(x1, y1, z1) và B(x2, y2, z2) trong không gian Oxyz là: AB = √[(x2-x1)² + (y2-y1)² + (z2-z1)²].
Khoảng cách từ điểm đến đường thẳng
Để tính khoảng cách từ điểm M đến đường thẳng d, ta cần tìm hình chiếu H của M lên d. Khoảng cách MH chính là khoảng cách cần tìm.
Khoảng cách từ điểm đến mặt phẳng
Đây là một dạng bài toán thường gặp trong các đề thi. Chúng ta có thể sử dụng công thức hoặc phương pháp hình chiếu để tính khoảng cách này.
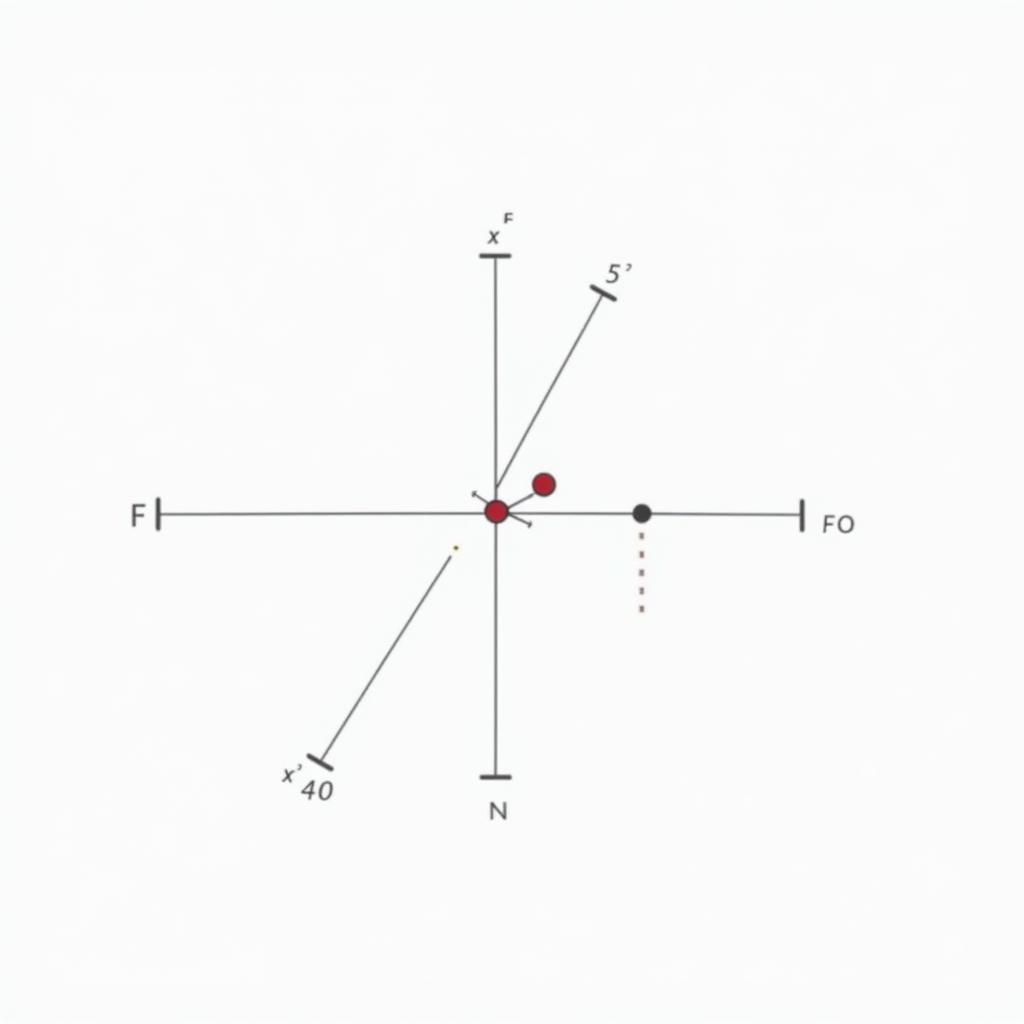Hình ảnh minh họa khoảng cách từ một điểm đến mặt phẳng trong không gian ba chiều
Khoảng cách giữa hai đường thẳng chéo nhau
Việc tính toán khoảng cách giữa hai đường thẳng chéo nhau đòi hỏi sự vận dụng linh hoạt các kiến thức về hình học không gian.
Cô Nguyễn Thị B, giáo viên Toán trường THPT Chu Văn An, Hà Nội, chia sẻ: “Học sinh thường gặp khó khăn khi tính khoảng cách giữa hai đường thẳng chéo nhau. Bí quyết nằm ở việc xác định đúng đường vuông góc chung của hai đường thẳng đó.”
Ứng Dụng Của Khoảng Cách Hình Học
Khoảng cách hình học không chỉ là một khái niệm toán học khô khan mà còn có rất nhiều ứng dụng trong thực tiễn, từ việc đo đạc trong xây dựng, thiết kế đến các lĩnh vực khoa học công nghệ cao.
Minh họa ứng dụng của khoảng cách hình học trong thiết kế và xây dựng
Mẹo Học Hiệu Quả
Theo quan niệm dân gian, việc học hành cũng cần có chút “tâm linh”. Trước khi bắt đầu học bài, hãy thắp một nén nhang, cầu mong cho trí tuệ minh mẫn, học hành tấn tới. Đừng quên giữ cho tinh thần thoải mái, học tập đúng giờ giấc.
Bạn cần hỗ trợ thêm?
Hãy liên hệ Số Điện Thoại: 0372888889, hoặc đến địa chỉ: 335 Nguyễn Trãi, Thanh Xuân, Hà Nội. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về khoảng cách hình học 11 trên tài liệu Violet. Chúc bạn học tập tốt và đạt được nhiều thành công! Hãy để lại bình luận và chia sẻ bài viết nếu bạn thấy hữu ích nhé! Và đừng quên khám phá thêm nhiều nội dung thú vị khác trên website HỌC LÀM.
