“배움은 실천과 함께”라는 옛말이 있듯이, 이론만 배우는 것이 아니라 배운 지식을 실제로 적용하는 것이 중요합니다. 특히 수학에서는 더욱 그렇습니다. 학생용 종이에 수학 도형을 그리는 것은 지식을 습득하고 개념을 명확히 이해하며 논리적 사고 능력을 키우는 효과적인 방법입니다.
삼각형 그리기
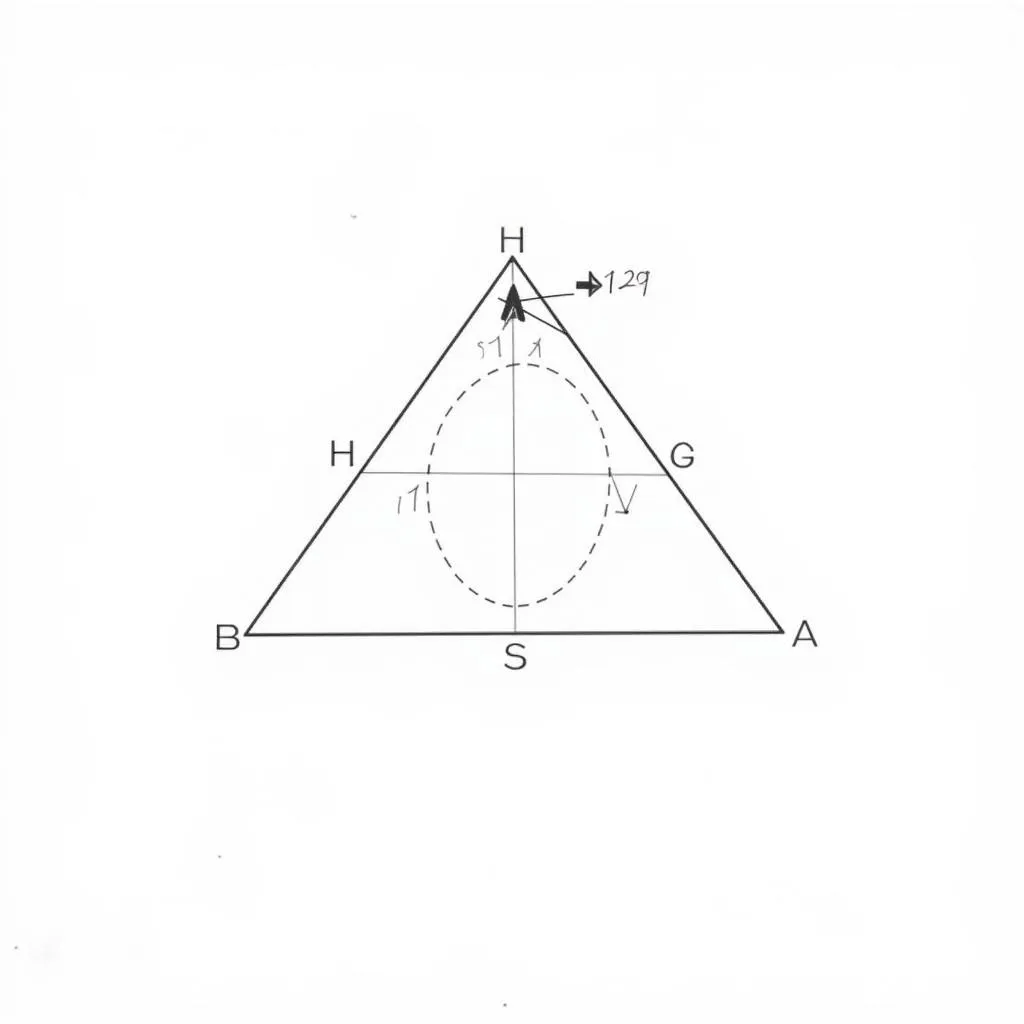
이등변삼각형 그리는 방법
이등변삼각형을 그리려면 학생용 종이, 연필, 자, 컴퍼스가 필요합니다.
1단계: 선분 AB를 이등변삼각형의 밑변으로 그립니다.
2단계: 컴퍼스를 사용하여 반지름이 AB와 같은 두 개의 원호를 그립니다. 각각의 원호의 중심은 A와 B입니다. 이 두 원호는 점 C에서 교차합니다.
3단계: A와 C, B와 C를 연결하면 이등변삼각형 ABC가 완성됩니다.
주의: 이등변삼각형은 두 변의 길이가 같고 밑각의 크기가 같습니다.
직각삼각형 그리는 방법
1단계: 선분 AB를 직각삼각형의 한 직각변으로 그립니다.
2단계: 자를 사용하여 점 A에서 AB에 수직인 직선을 그립니다.
3단계: 수직선 위에 점 C를 찍어 AC의 길이가 직각삼각형의 다른 직각변의 길이와 같게 합니다.
4단계: B와 C를 연결하면 직각삼각형 ABC가 완성됩니다.
주의: 직각삼각형은 한 각이 직각(90도)입니다.
사각형 그리기
정사각형 그리는 방법
1단계: 선분 AB를 정사각형의 한 변으로 그립니다.
2단계: 자를 사용하여 점 A에서 AB에 수직인 직선을 그립니다.
3단계: 수직선 위에 점 C를 찍어 AC의 길이가 AB와 같게 합니다.
4단계: 컴퍼스를 사용하여 반지름이 AB와 같고 중심이 C인 원호를 그립니다. 이 원호는 수직선과 점 D에서 교차합니다.
5단계: B와 C, C와 D, D와 A를 연결하면 정사각형 ABCD가 완성됩니다.
주의: 정사각형은 네 변의 길이가 같고 네 각이 직각입니다.
직사각형 그리는 방법
1단계: 선분 AB를 직사각형의 가로 길이로 그립니다.
2단계: 자를 사용하여 점 A에서 AB에 수직인 직선을 그립니다.
3단계: 수직선 위에 점 C를 찍어 AC의 길이가 직사각형의 세로 길이와 같게 합니다.
4단계: 컴퍼스를 사용하여 반지름이 AB와 같고 중심이 C인 원호를 그립니다. 이 원호는 수직선과 점 D에서 교차합니다.
5단계: B와 C, C와 D, D와 A를 연결하면 직사각형 ABCD가 완성됩니다.
주의: 직사각형은 마주보는 두 변의 길이가 같고 네 각이 직각입니다.
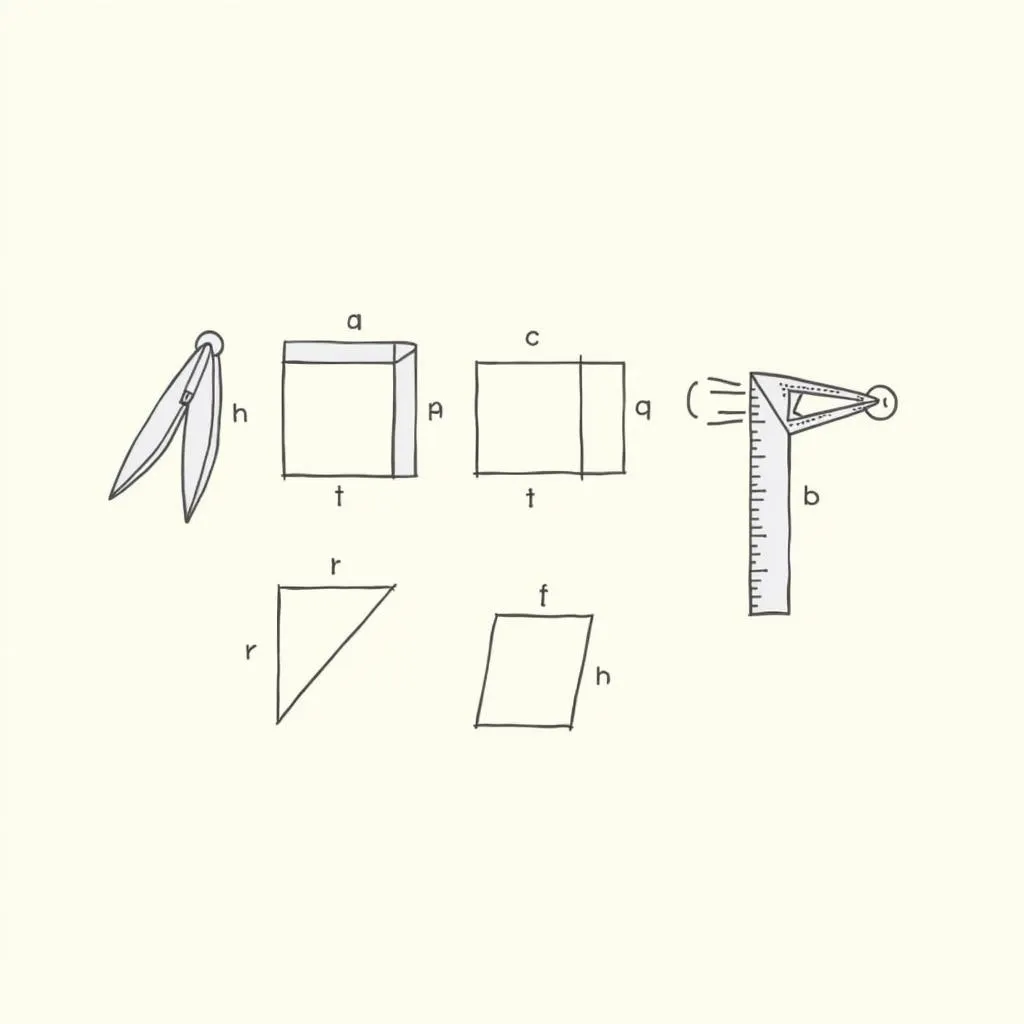 정사각형과 직사각형 그리는 방법
정사각형과 직사각형 그리는 방법
원 그리기
원 그리는 방법
1단계: 컴퍼스를 사용하여 컴퍼스 바늘을 종이 위의 점 O에 놓습니다.
2단계: 컴퍼스를 원하는 원의 반지름만큼 벌립니다.
3단계: 컴퍼스 바늘을 점 O에 고정하고 컴퍼스를 한 바퀴 돌립니다.
주의: 원은 중심에서 같은 거리에 있는 모든 점들의 집합입니다.
수학 도형을 그릴 때 유의해야 할 점
- 항상 자와 컴퍼스를 사용하여 정확하게 도형을 그리십시오.
- 도형을 그릴 때 주의를 기울여 깔끔하고 선명하게 그리십시오.
- 연필로 그리고 필요하면 펜으로 선을 강조할 수 있습니다.
- 학생용 종이에 도형을 그리면 메모하고 분석하기 쉽습니다.
- 그림을 다 그린 후에는 변과 각을 다시 확인하여 정확성을 확인하십시오.
수학 도형 그리기의 중요성
“수학 – 성공으로 가는 길”의 저자 응우옌 반 A 선생님은 “수학 도형 그리기는 지식을 습득하는 데 도움이 될 뿐만 아니라 논리적 사고 능력과 공간 상상력을 키우고 문제 해결 능력을 향상시킵니다.”라고 말합니다.
도형 그리기는 학습 효율성을 높이는 데도 기여합니다. 베트남 최고의 교육 전문가 부 딘 뚜옌 교수는 “도형 그리기는 수학 학습에서 효과적인 학습 방법입니다. 도형을 그리면 개념, 정리, 공식을 쉽게 기억할 수 있습니다. 따라서 수학 문제 풀이에 더 자신감을 가질 수 있습니다.”라고 단언합니다.
 수학 도형을 그리는 학생
수학 도형을 그리는 학생
자주 묻는 질문
- 가장 정확하게 원을 그리는 방법은 무엇입니까?
- 비법은 컴퍼스를 돌릴 때 컴퍼스 바늘을 점 O에 고정하는 것입니다.
- 가로 길이가 세로 길이의 두 배인 직사각형을 어떻게 그리나요?
- 세로 길이를 가로 길이의 1/2로 그려야 합니다.
- 정삼각형은 어떻게 그리나요?
- 정삼각형을 그리려면 컴퍼스와 자를 사용해야 합니다.
- 학생용 종이에 입방체나 구와 같은 더 복잡한 수학 도형을 그릴 수 있나요?
- 기본 도형을 결합하여 더 복잡한 도형을 그릴 수 있습니다.
- 수학 도형 그리기는 학습에 어떤 도움이 되나요?
- 도형을 그리면 지식을 시각화하고 기억하며 논리적 사고력을 키울 수 있습니다.
결론
학생용 종이에 수학 도형을 그리는 것은 수학을 잘하고 논리적 사고력을 키우는 데 도움이 되는 중요한 기술입니다. 최고의 학습 결과를 얻으려면 도형 그리기 기술을 열심히 연습하십시오.
웹사이트 HỌC LÀM에서 더 복잡한 수학 도형을 그리는 방법에 대해 자세히 알아볼 수 있습니다. 성공을 기원합니다!